FIN435 • Term Project — Efficient Frontier

Stock Data Web App students build it

This Google Apps Script web app writes daily close prices into a Google Sheet (via GOOGLEFINANCE()). Then students convert to month-end closes and compute monthly returns.

Open Stock Data App → How to use the data Back to files

Copy/paste URL (if the button won’t open)

URL: https://script.google.com/macros/s/AKfycbxao_yHFToaMAs2fuEiYMfHapioFAjIukvBAFyJIOS6ccYL2WAepMMyrO8afpRjsVBA/exec

How to create your own copy (so you own the Sheet + code)

Create a new Google Sheet (this is where the data will go).
In that Sheet: Extensions → Apps Script.
In Code.gs, paste the server code (below).
Add an HTML file named Index, paste the UI code (below).
Deploy: Deploy → New deployment → Web app.
Execute as: Me. Who has access: Anyone with the link (or class choice).
Authorize the script when Google asks.
Copy the new /exec URL and share it.

Code (copy/paste) — Web app UI (Index.html)

<!DOCTYPE html>
<html>
<head>
  <base target="_top">
  <meta name="viewport" content="width=device-width, initial-scale=1">
  <title>Stock Data Fetcher</title>
  <style>
    body{font-family:Arial,sans-serif;margin:20px}
    h2{color:#333;margin:0 0 8px}
    p{line-height:1.45;color:#444}
    label{display:block;margin-top:10px;font-weight:700}
    input,button{margin-top:5px}
    input{padding:8px 10px;border:1px solid #ddd;border-radius:10px;width:100%;max-width:360px}
    button{padding:10px 12px;border:0;border-radius:10px;background:#2e7d32;color:#fff;font-weight:800;cursor:pointer;margin-top:12px}
    button:hover{filter:brightness(1.03)}
    #status{margin-top:10px;color:#555}
    .description{background:#f9f9f9;border:1px solid #ddd;padding:10px;margin-top:20px;border-radius:10px}
    .footer{margin-top:20px;font-size:12px;color:#666;text-align:center}
  </style>
</head>

<body>
  <h2>Stock Data Fetcher</h2>

  <p>
    Use this app to fetch <strong>daily closing prices</strong> for a ticker over a date range.
    Then convert to <strong>month-end closes</strong> and compute <strong>monthly returns</strong> in the Google Sheet.
  </p>

  <label for="ticker">Stock Ticker:</label>
  <input type="text" id="ticker" placeholder="e.g., AAPL, WMT" />

  <label for="startDate">Start Date:</label>
  <input type="date" id="startDate" />

  <label for="endDate">End Date:</label>
  <input type="date" id="endDate" />

  <button onclick="fetchData()">Fetch Data</button>
  <p id="status"></p>

  <button onclick="openGoogleSheet()">Open Google Sheet</button>

  <div class="description">
    <h3>Explanation of Google Sheet Structure</h3>
    <p>After fetching the stock data, it will appear in your Google Sheet like this:</p>

    <ul>
      <li><strong>Column A:</strong> Date of each trading day within the selected range.</li>
      <li><strong>Column B:</strong> Closing price on each trading day.</li>
      <li><strong>Column D:</strong> Company name (from the ticker).</li>
      <li><strong>Columns F, G, and H:</strong>
        <ul>
          <li><strong>Column F:</strong> Last trading day of each month.</li>
          <li><strong>Column G:</strong> Month-end closing price.</li>
          <li><strong>Column H:</strong> Monthly return (% change from prior month-end to current month-end).</li>
        </ul>
      </li>
    </ul>

    <p><strong>Purpose:</strong> Quickly build clean month-end returns for your efficient frontier project.</p>
  </div>

  <div class="footer">© 2024 Stock Data Fetcher</div>

  <script>
    function fetchData(){
      var ticker = document.getElementById('ticker').value.trim();
      var startDate = document.getElementById('startDate').value;
      var endDate = document.getElementById('endDate').value;

      document.getElementById('status').innerText = "Running...";
      google.script.run.withSuccessHandler(function(response){
        document.getElementById('status').innerText = response;
      }).fetchStockData(ticker, startDate, endDate);
    }

    function openGoogleSheet(){
      // Replace with your actual Google Sheet URL (this one is your current link)
      var sheetUrl = "https://docs.google.com/spreadsheets/d/1rsw8JJL4gglK51uCi5FiW7d0jFLQM9h_ceVcdsfGCqI/edit?gid=0#gid=0";
      window.open(sheetUrl, "_blank");
    }
  </script>
</body>
</html>

Project Files

Links below use relative filenames. Upload the files into the same folder as this page, then rename link targets if needed.

Required

FYI (examples)

Tip: Use the NO IFERROR version if you’re stuck — it reveals where the Excel formulas break so you can fix the reference.

Image

Note (important)

The efficient frontier is the set of optimal portfolios that offer the highest expected return for a given level of risk.
Visualizing the frontier helps you see the trade-off between risk and return and supports better decisions.
If Solver returns no results, try adding constraints. Example: each weight is between 5% and 30%.

What your results should say

Key findings (example output)

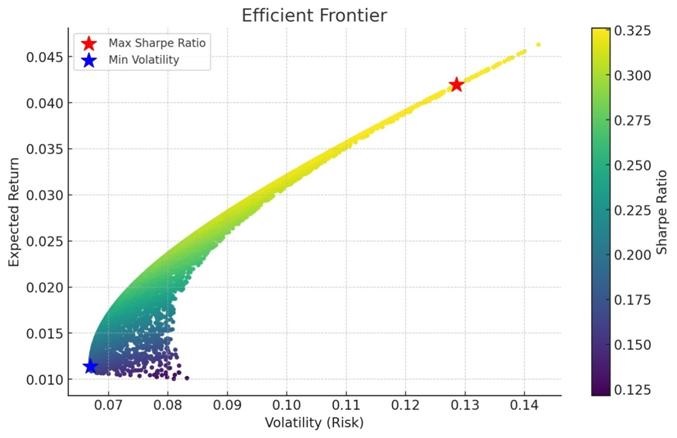
1) Max Sharpe Ratio Portfolio (best risk-adjusted return)

Expected Return: 4.19%
Volatility (Risk): 12.85%
Sharpe Ratio: 0.326

2) Min Volatility Portfolio (lowest risk)

Expected Return: 1.14%
Volatility (Risk): 6.70%
Sharpe Ratio: 0.170

Takeaways

The Efficient Frontier shows the best possible portfolios at different risk levels.
Higher returns require accepting more risk.
The Max Sharpe portfolio provides the best balance of return per unit of risk.
The Minimum Volatility portfolio is safest, but returns are lower.
Sharpe Ratio helps compare risk-adjusted returns — higher is better.

Plain-English explanation

The goal of the efficient frontier is to help investors identify the portfolio that provides the maximum return for a given level of risk, or the minimum risk for a given level of return. By plotting many portfolios, you can see the best risk–return trade-offs and choose the portfolio that matches your objectives.

🎥 Class recording — Efficient Frontier (Excel + Solver)

If you’re stuck, watch this first. It’s the full class walkthrough (data → returns → covariance → Solver → frontier plot).

▶ Open the class video (full-screen) Then follow the checklist ↓

Class Recording

Step-by-step checklist

Steps (do these in order)

Data collection: monthly close prices for 8 securities (Yahoo Finance, or use the Stock Data Web App + Sheet).
Monthly returns: compute month-to-month returns for each security.
Statistical analysis: average monthly return + standard deviation (monthly).
Annualize: annual return and annual volatility from monthly data.
Correlation: build the 8×8 correlation matrix in Excel.
Covariance matrix: convert correlations + σ’s into covariances (or use Excel’s covariance functions).
Equally weighted portfolio: weights = 1/8 each → compute E[Rp] and σp.
Solver analysis: minimize portfolio σp subject to (a) weights sum to 1, (b) weights bounds (e.g., 5%–30%), and (c) a target E[Rp].
Efficient frontier: repeat Solver for many target returns; plot (σp, E[Rp]) points and connect the “upper-left” boundary.
Write-up: summarize your best risk-adjusted portfolio (max Sharpe) and your lowest-risk portfolio (min volatility).

Formulas (8-stock portfolio)

Portfolio return

Portfolio Return = w1*r1 + w2*r2 + w3*r3 + w4*r4 + w5*r5 + w6*r6 + w7*r7 + w8*r8

Weights w1…w8 sum to 1, and r1…r8 are the (annualized) expected returns.

Portfolio risk

Portfolio Standard Deviation = √(wᵀΣw)

Σ is the 8×8 covariance matrix. This is the cleanest way to do the 8-stock calculation in Excel.

Expanded portfolio risk formula + covariance (what it is)

σp = √( w1²σ1² + w2²σ2² + w3²σ3² + w4²σ4² + w5²σ5² + w6²σ6² + w7²σ7² + w8²σ8²

+ 2w1w2ρ12σ1σ2 + 2w1w3ρ13σ1σ3 + 2w1w4ρ14σ1σ4 + 2w1w5ρ15σ1σ5 + 2w1w6ρ16σ1σ6 + 2w1w7ρ17σ1σ7 + 2w1w8ρ18σ1σ8
+ 2w2w3ρ23σ2σ3 + 2w2w4ρ24σ2σ4 + 2w2w5ρ25σ2σ5 + 2w2w6ρ26σ2σ6 + 2w2w7ρ27σ2σ7 + 2w2w8ρ28σ2σ8
+ 2w3w4ρ34σ3σ4 + 2w3w5ρ35σ3σ5 + 2w3w6ρ36σ3σ6 + 2w3w7ρ37σ3σ7 + 2w3w8ρ38σ3σ8
+ 2w4w5ρ45σ4σ5 + 2w4w6ρ46σ4σ6 + 2w4w7ρ47σ4σ7 + 2w4w8ρ48σ4σ8
+ 2w5w6ρ56σ5σ6 + 2w5w7ρ57σ5σ7 + 2w5w8ρ58σ5σ8
+ 2w6w7ρ67σ6σ7 + 2w6w8ρ68σ6σ8
+ 2w7w8ρ78σ7σ8 )

What is covariance (Cov)?
Covariance measures how two assets’ returns move together. Since you already know correlation: Cov(i,j) = Corr(i,j) × σi × σj. Also, the diagonal is: Cov(i,i) = σi².

• If Corr(i,j) is positive, the two assets tend to move in the same direction → covariance is positive.
• If Corr(i,j) is negative, they tend to move in opposite directions → covariance is negative.
• Difference: correlation is standardized (between −1 and +1); covariance is in “return units” and depends on σ.

In Excel: Cov(i,j) = Corr(i,j) * StDev(i) * StDev(j)

Using the covariance matrix avoids typing dozens of pairwise terms.

CML (Capital Market Line) — Optional

How to draw a tangent line from Rf to the Efficient Frontier

Determine the risk-free rate (e.g., Treasury bill yield).
Find the portfolio with the highest Sharpe ratio.
The slope of the tangent line equals that Sharpe ratio.
Draw the tangent line from Rf (y-axis) to the tangency point on the frontier.

This tangent line is called the Capital Market Line (CML). Any portfolio on the CML is a combination of the risk-free asset and the tangency portfolio.

8-Stock Efficient Frontier Tool interactive

Use this tool to visualize random portfolios + the efficient frontier for 8 assets.

Open 8-Stock Efficient Frontier →

URL: https://www.jufinance.com/game/eight_stock_risk_return.html